Chapter 5 Minerals
Adapted from Physical Geology, First University of Saskatchewan Edition (Karla Panchuk) and Physical Geology (Steven Earle)
. Click the image for more attributions._](figures/05-minerals/figure-5-1.png)
Figure 5.1: Giant crystals of gypsum in the Naica Mine in Mexico. The crystals formed in volcanically heated water, and became accessible when the cave was drained as part of mining activities. The cave was very hot, making it fatal for visitors to enter without cooling equipment and respirators. When mining activities ceased, caverns were allowed to flood again. Source: Karla Panchuk CC BY-NC-SA 4.0. Photograph- Paul Williams (2009) CC BY-NC 2.0 view source. Click the image for more attributions.
Learning Objectives
After reading this chapter and answering the review questions at the end, you should be able to:
- List the criteria required for a substance to be considered a mineral.
- Explain how atoms bond within minerals.
- Explain how mineral lattices influence the properties of minerals.
- Summarize the categories of minerals defined by anions or anionic groups.
- Describe the types of configurations of silica tetrahedra found in silicate minerals.
- Explain how minerals form.
- Describe the key properties for identifying minerals.
5.0.1 What Is a Mineral?
Minerals are all around us: the graphite in your pencil, the salt on your table, the plaster on your walls, and the trace amounts of gold in your computer. Minerals can be found in a wide variety of consumer products such as paper, medicine, processed foods, and cosmetics. And of course, everything made of metal is also derived from minerals.
A mineral is a naturally occurring solid made of specific elements, and arranged in a particular repeating three-dimensional structure.
“Naturally occurring” means that minerals can be formed from substances and under conditions found in nature. Substances that can only be made by humans—classified as anthropogenic materials—do not count as minerals, nor do substances produced by natural processes acting upon anthropogenic materials.
In the context of the definition of minerals, “solid” means solid at 25ºC. There are some exceptions to this rule, made for substances defined as minerals before 1959, prior to strict procedures being established for determining what is or isn’t a mineral. One example is ice, which is only solid at or below 0 °C. Another is mercury, which is solid below -39 ºC. Mercury that is present in rocks at temperatures above -39 ºC appears as silvery blobs of liquid (Figure 5.2).
_](figures/05-minerals/figure-5-2.jpeg)
Figure 5.2: Droplets of native mercury (pure mercury, Hg), also called quicksilver, amid waxy red crystals of cinnabar (HgS). Cinnabar is a mercury ore mineral. Source: Parent Géry (2012) CC BY-SA 3.0 view source
“Specific elements” means that minerals have a specific chemical formula or composition. The mineral pyrite, for example, is FeS2 (two atoms of sulphur for each atom of iron), and any significant departure from that formula would make it a different mineral. Some minerals can have variable compositions within a specific range. The mineral olivine, for example, has a formula written as (Fe,Mg)2SiO4, because the composition of olivine can range all the way from Fe2SiO4 to Mg2SiO4, and have any proportion of iron and magnesium in between. This type of substitution is known as solid solution.
Most important of all, the atoms within a mineral are arranged in a specific repeating three-dimensional structure or lattice. This regular structure means that all minerals are crystals. The mineral halite, which we use as table salt, has a relatively simple crystal lattice (Figure 5.3). Atoms of sodium (Na, purple) alternate with atoms of chlorine (Cl, green). The chemical bonds holding the Na and Cl atoms together are all at 90º to each other. Even tiny crystals, like the ones in your salt shaker, have lattices that extend in three dimensions for thousands of repetitions. Halite will always have this structure, and will always have the formula NaCl.
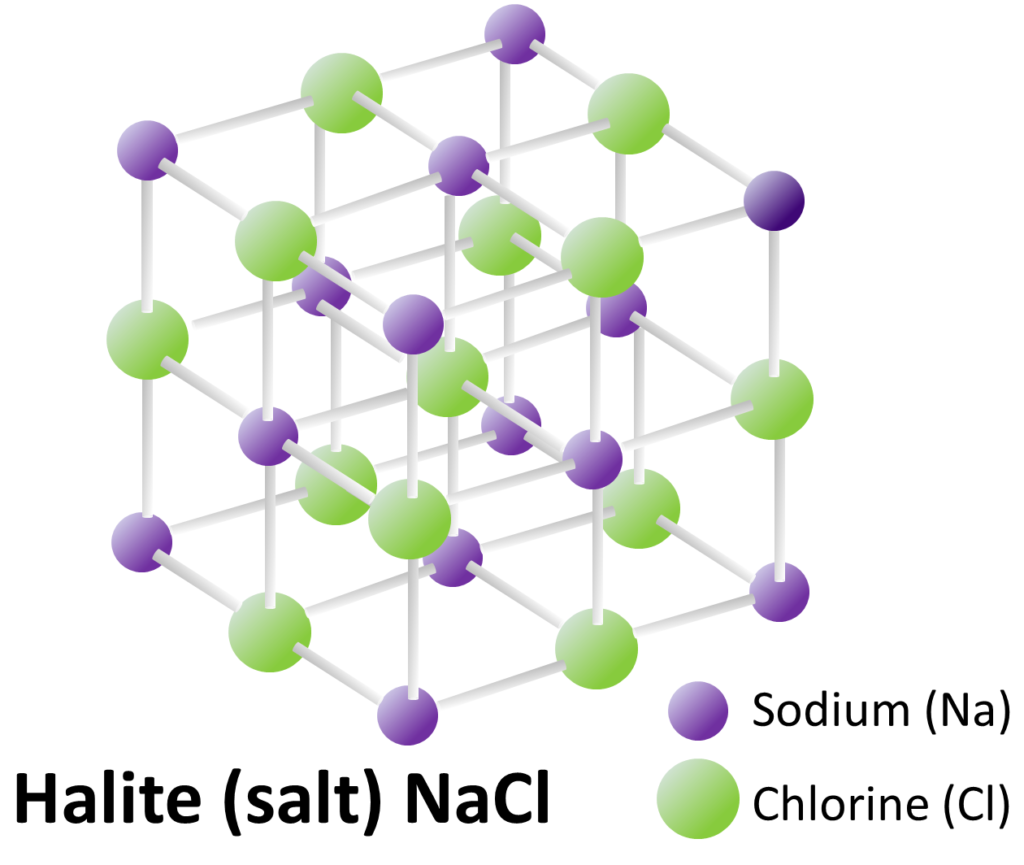
Figure 5.3: Halite crystal lattice. Halite is the mineral in table salt. Source: Steven Earle (2015) CC BY 4.0
Some mineral-like materials do not have a regular internal atomic arrangement. Opal (Figure 5.4) is one example. In many respects it fits the definition of a mineral: it has a specific chemical composition (SiO2·_n_H2O, where n means that there can be varying amounts of water in the structure), forms naturally through geological processes, and is solid at 25 ºC. However, the structure of opal consists of closely packed spheres (Figure 5.4, right) rather than a lattice like halite. Substances like opal, which are mineral-like, but which do not have a crystalline structure, are called mineraloids.
; Right- Mineralogy Division, Geological and Planetary Sciences, Caltech (n.d.) CC BY-NC [view source](http://minerals.gps.caltech.edu/COLOR_Causes/Physical_Process/opal-beads_40k.jpg)/ [view context](http://minerals.gps.caltech.edu/COLOR_Causes/Physical_Process/index.htm)_](figures/05-minerals/figure-5-4.png)
Figure 5.4: Opal is mineral-like, but does not have a crystalline structure. Instead, it is made up of layers of closely packed spheres (right). Source: Left- James St. John (2016) CC BY 2.0 view source; Right- Mineralogy Division, Geological and Planetary Sciences, Caltech (n.d.) CC BY-NC view source/ view context
Note: Element symbols such as Na and Cl are used extensively in this book. In Appendix A you can find a list of the symbols, the names of the elements common in minerals, and a copy of the periodic table of elements.
5.1 Atoms
5.1.1 Protons Are What Make Elements Distinct
All matter, including mineral crystals, is made up of atoms. All atoms are made up of three main particles: protons, neutrons, and electrons. Protons have a positive charge, neutrons have no charge, and electrons have a negative charge. Protons and neutrons have approximately the same mass, but electrons have a mass that is 10,000 times smaller.
The element hydrogen (H) has the simplest atoms. Most hydrogen atoms have just one proton and one electron. The proton forms the nucleus (the centre of the atom), while the electron orbits around it (Figure 5.5, left). All other elements have more than one proton in their nucleus. Protons repel each other because they are positively charged, but it is possible to have more than one proton in a nucleus because neutrons hold them together. The next most complex atom, helium (He) has two protons and two neutrons in its nucleus, in its most common form. Some atoms of the same element can have different numbers of neutrons. For example, forms of hydrogen exist with one and two neutrons, and a tiny fraction of He atoms have only one neutron. Forms of an element with different numbers of neutrons are called isotopes.
_](figures/05-minerals/figure-5-5.png)
Figure 5.5: Atomic structure of hydrogen and helium showing protons (p+), neutrons (n), and electrons (e-). Source: Bruce Blaus (2014) CC BY 3.0 view source
The number of protons in an atom determines what element it will be, so the number of protons is called the atomic number of that element. The total number of protons and neutrons in the nucleus is the mass number. The mass number distinguishes between isotopes of an element. Isotopes of an element are denoted by putting the mass number as a subscript in front of the symbol for that element. For example, the isotopes of hydrogen are 1H (1 proton), 2H (1 proton + 1 neutron), and 3H (1 proton + 2 neutrons).
For most of the 16 lightest elements (up to oxygen) the number of neutrons is equal to the number of protons. For most of the remaining elements, there are more neutrons than protons. This is because the more protons that are concentrated in a small space, the more neutrons are needed to keep the nucleus together. The most common isotope of uranium (U), for example, is 238U. It has 92 protons, but requires 146 neutrons to keep them together. The neutrons are only partly successful. Uranium is radioactive, meaning that its nucleus will eventually split apart and release energy. What remains of the nucleus has fewer protons, so after decay the atom is a different element.
5.1.2 Electrons Are What Control How Atoms Interact
Electrons orbiting around the nucleus of an atom are arranged in shells (also called energy levels). The first shell can hold only two electrons (as in H and He in Figure 5.5), but the next shell holds up to eight electrons. An atom can have many shells of electrons, but there are never more than 8 outermost electrons interacting with surrounding atoms.
The outermost electrons determine how atoms can be bonded together. Elements that have a full outer shell (e.g., neon, Figure 5.6 right) are inert because they do not react with other elements to form compounds. These are the noble gases (including helium, argon, krypton, and radon, in addition to neon) in the far-right column of the periodic table. For elements that do not have a full outer shell (e.g., lithium, Figure 5.6 left), the outermost electrons can interact with the outermost electrons of nearby atoms to create chemical bonds.
_](figures/05-minerals/figure-5-6.png)
Figure 5.6: The number of electrons in an atom’s outermost shell (or energy level) determine whether it will bond to other atoms, and how it will bond. Right- Neon has a completely filled outer shell with 8 electrons. It does not bond with other atoms. Left- Lithium has only one electron in its outer shell. It bonds with other atoms. Source: Bruce Blaus (2014) CC BY 3.0 view source
The electron shell configurations for 29 of the first 36 elements are listed in Table 5.1. Note that some of the shells in the table below have more than 8 electrons. This is because they contain subshells. For example, the third shell can hold up to 18 electrons because it contains one subshell that can hold 2 electrons, and two subshells that can hold 8 electrons each.
| Element | Symbol | Atomic Number | First | Second | Third | Fourth |
|---|---|---|---|---|---|---|
| Hydrogen | H | 1 | 1 | |||
| Helium | He | 2 | 2 | |||
| Lithium | Li | 3 | 2 | 1 | ||
| Beryllium | Be | 4 | 2 | 2 | ||
| Boron | B | 5 | 2 | 3 | ||
| Carbon | C | 6 | 2 | 4 | ||
| Nitrogen | N | 7 | 2 | 5 | ||
| Oxygen | O | 8 | 2 | 6 | ||
| Fluorine | F | 9 | 2 | 7 | ||
| Neon | Ne | 10 | 2 | 8 | ||
| Sodium | Na | 11 | 2 | 8 | 1 | |
| Magnesium | Mg | 12 | 2 | 8 | 2 | |
| Aluminum | Al | 13 | 2 | 8 | 3 | |
| Silicon | Si | 14 | 2 | 8 | 4 | |
| Phosphorus | P | 15 | 2 | 8 | 5 | |
| Sulphur | S | 16 | 2 | 8 | 6 | |
| Chlorine | Cl | 17 | 2 | 8 | 7 | |
| Argon | Ar | 18 | 2 | 8 | 8 | |
| Potassium | K | 19 | 2 | 8 | 8 | 1 |
| Calcium | Ca | 20 | 2 | 8 | 8 | 2 |
| Scandium | Sc | 21 | 2 | 8 | 9 | 2 |
| Titanium | Ti | 22 | 2 | 8 | 10 | 2 |
| Vanadium | V | 23 | 2 | 8 | 11 | 2 |
| Chromium | Cr | 24 | 2 | 8 | 13 | 1 |
| Manganese | Mn | 25 | 2 | 8 | 13 | 2 |
| Iron | Fe | 26 | 2 | 8 | 14 | 2 |
| . | . | . | . | . | . | . |
| Selenium | Se | 34 | 2 | 8 | 18 | 6 |
| Bromine | Br | 35 | 2 | 8 | 18 | 7 |
| Krypton | Kr | 36 | 2 | 8 | 18 | 8 |
5.2 Bonding and Lattices
Atoms seek to have a full outer shell. For hydrogen and helium, a full outer shell means two electons. For other elements, it means 8 electrons. Filling the outer shell is accomplished by transferring or sharing electrons with other atoms in chemical bonds. The type of chemical bond is important for the study of minerals because the type of bond will determine many of a mineral’s physical and chemical properties.
5.2.1 Ionic Bonds
Consider the example of halite again, which is made up of sodium (Na) and chlorine (Cl). Na has 11 electrons: two in the first shell, eight in the second, and one in the third (Figure 5.7, top). Na readily gives up the third shell electron so it can have the second shell with 8 electrons as its outermost shell. When it loses the electron, the total charge from the electrons is -10, but the total charge from the protons is +11, so it is left with a +1 charge over all.
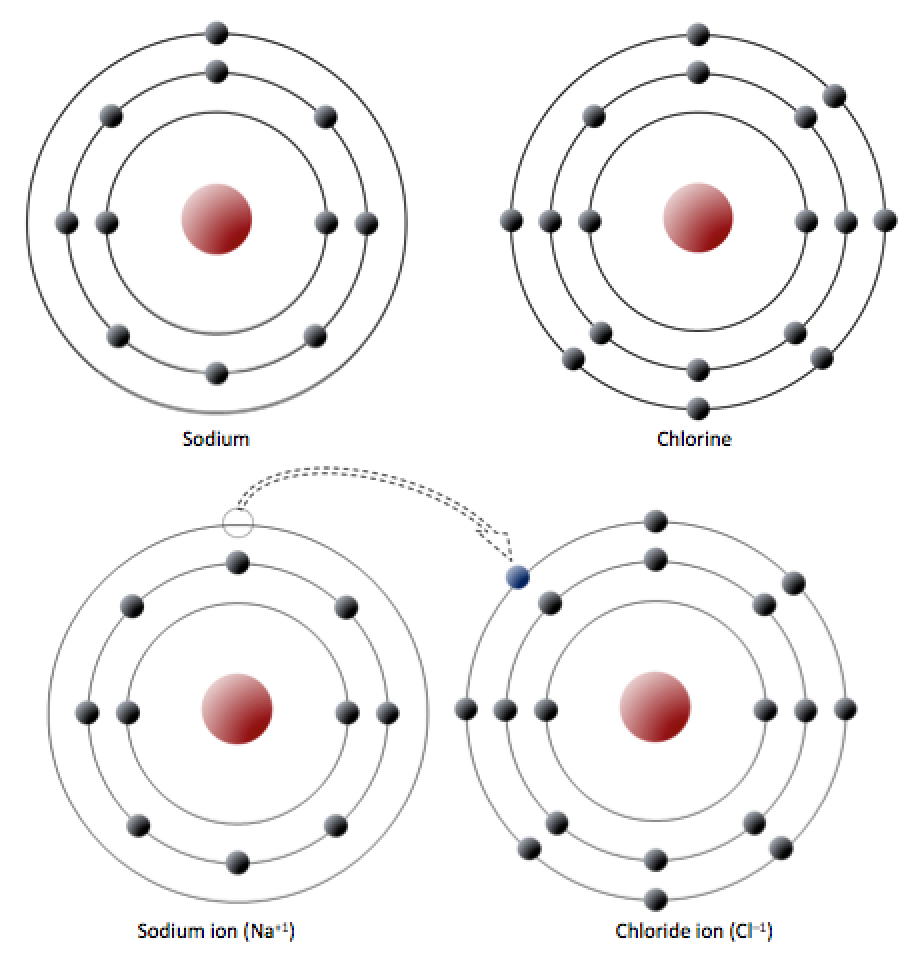_](figures/05-minerals/figure-5-7.png)
Figure 5.7: Electron configuration of sodium and chlorine atoms (top). Sodium gives up an electron to become a cation (bottom left) and chlorine accepts an electron to become an anion (bottom right). Source: Steven Earle (2015) CC BY 4.0 view source
Chlorine has 17 electrons: two in the first shell, eight in the second, and seven in the third. Cl readily accepts an eighth electron to fill its third shell, and therefore becomes negatively charged because it has a total charge of -18 from electrons, and a total charge of +17 from protons.
In changing their number of electrons, these atoms become ions — the sodium loses an electron to become a positive ion or cation,4 and the chlorine gains an electron to become a negative ion or anion (Figure 5.7, bottom). Because negative and positive charges attract, sodium and chlorine ions stick together, creating an ionic bond. In an ionic bond, electrons can be thought of as having transferred from one atom to another.
Exercise: Cation or Anion?
A number of elements are listed below along with their atomic numbers (the number of protons, and therefore also the number of electrons in the atom). Assuming that the first electron shell can hold two electrons and subsequent electron shells can hold eight electrons, sketch the electron configurations for these elements, as in the example for fluorine (Figure 5.8). If you fill a shell and have electrons left over, draw another shell around the atom. Predict whether the element is likely to form a cation or an anion, and what charge it would have (e.g., +1, +2, –1).
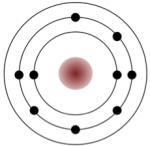_](figures/05-minerals/figure-5-8.png)
Figure 5.8: How to draw the electron configuration for fluorine, with an atomic number of 9. Source: Karla Panchuk (2018) CC BY 4.0, modified after Steven Earle (2015) CC BY 4.0 view source
- Lithium (3)
- Magnesium (12)
- Argon (18)
- Chlorine (17)
- Beryllium (4)
- Oxygen (8)
- Sodium (11)
5.2.2 Covalent Bonds
An element like chlorine can also form bonds without forming ions. For example, two chlorine atoms can each complete their outer shells by sharing electrons. Chlorine gas (Cl2, Figure 5.9) is formed when two chlorine atoms form a covalent bond.
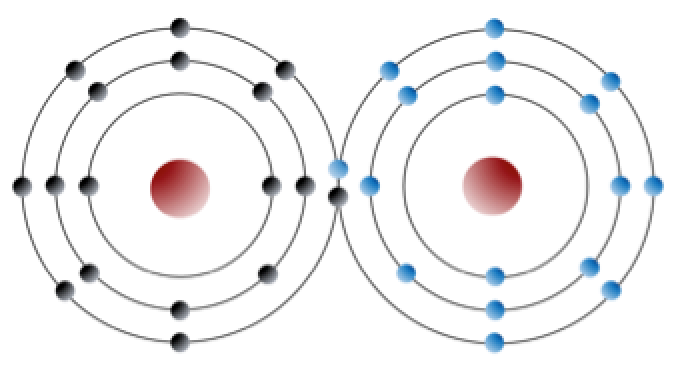_](figures/05-minerals/figure-5-9.png)
Figure 5.9: A covalent bond between two chlorine atoms. The electrons are black in the left atom, and blue in the right atom. Two electrons are shared (one black and one blue) so that each atom appears to have a full outer shell. Source: Steven Earle (2015) CC BY 4.0 view source
Carbon is another atom that participates in covalent bonding. An uncharged carbon atom has six protons and six electrons. Two of the electrons are in the inner shell and four are in the outer shell (Figure 5.10, left). Carbon would need to gain or lose four electrons to have a filled outer shell, and this would create too great a charge imbalance. Instead, carbon atoms share electrons to create covalent bonds (Figure 5.10, right).
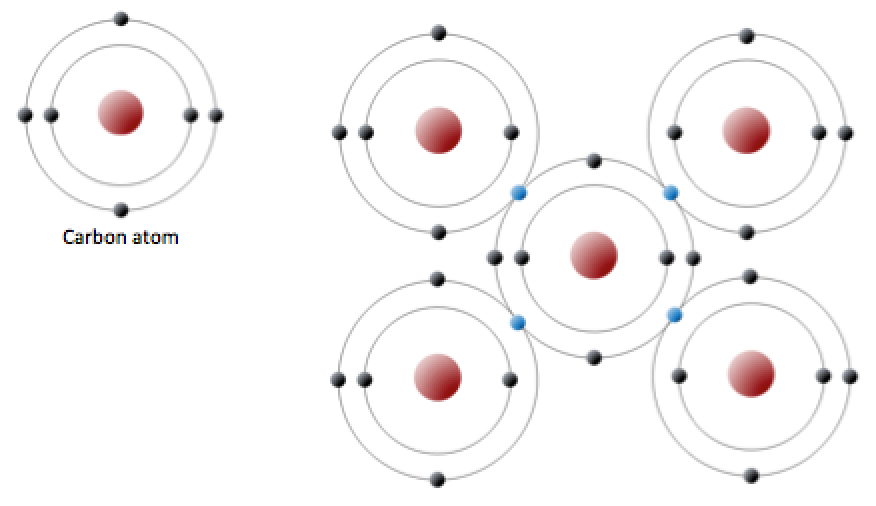_](figures/05-minerals/figure-5-10.png)
Figure 5.10: The electron configuration of carbon (left) and the sharing of electrons in covalent C bonding (right). The electrons shown in blue are shared between adjacent C atoms. Source: Steven Earle (2015) CC BY 4.0 view source
In the mineral diamond (Figure 5.11, left), the carbon atoms are linked together in a three-dimensional framework, where one carbon atom is bonded to four other carbon atoms, and every bond is a very strong covalent bond.
_](figures/05-minerals/figure-5-11.png)
Figure 5.11: Covalently bonded structures. Left: Diamond with three-dimensional structure of covalently bonded carbon. Right: Graphite with covalently bonded sheets of carbon. Sheets are held together by weaker van der Waals forces. Source: Karla Panchuk (2018) CC BY 4.0, modified after Materialscientist (2009) CC BY-SA 3.0 view source
5.2.3 Other Types of Bonds
Most minerals are characterized by ionic bonds, covalent bonds, or a combination of the two, but there are other types of bonds that are important in minerals. Consider the mineral graphite (Figure 5.11, right): the carbon atoms are linked together in sheets or layers in which each carbon atom is covalently bonded to three others. Graphite-based compounds are strong because of the covalent bonding between carbon atoms within each layer, which is why they are used in high-end sports equipment such as ultralight racing bicycles. Graphite itself is soft, however, because the layers themselves are held together by relatively weak Van der Waals forces.
Van der Waals forces, like hydrogen bonds, work because molecules can be electrostatically neutral, but still have an end that is slightly more positive and an end that is slightly more negative. In water molecules (Figure 5.12, left), the bent shape puts the hydrogen atoms on one side of the molecule, and the oxygen atom, with more electrons, on the other. The charge is distributed asymmetrically across the water molecule. Contrast this with the straight carbon dioxide (Figure 5.12, right) molecule. The slightly more negative oxygen atoms on the ends are distributed symmetrically on either side of the carbon atom.
 and Jynto (2011) CC0 1.0 [view source](https://commons.wikimedia.org/wiki/File:Carbon_dioxide_3D_ball.png)_](figures/05-minerals/figure-5-12.png)
Figure 5.12: Hydrogen bonding. Water molecules (left) are polar molecules (their charge is distributed asymmetrically). Slightly negative parts of the molecule are attracted to slightly positive parts of other water molecules. Carbon dioxide (right) is a non-polar molecule. The slightly negative oxygen atoms are distributed symmetrically on either side of the carbon atom. Source: Karla Panchuk (2018) CC BY-SA 4.0. Modified after Querter (2011) CC BY-SA 3.0 view source and Jynto (2011) CC0 1.0 view source
Metallic bonding occurs in metallic elements because they have outer electrons that are relatively loosely held. (The metals are highlighted on the periodic table in Appendix 1.) When bonds between such atoms are formed, the dissociated electrons can move freely from one atom to another. This feature accounts for two very important properties of metals: their electrical conductivity and their malleability (they can be deformed and shaped).
_](figures/05-minerals/figure-5-13.png)
Figure 5.13: Metallic bonding. Dissociated electrons (grey dots) move between metal atoms. Source: Karla Panchuk (2018) CC BY-SA 4.0. Nucleus by Fornax (2010) CC BY-SA 3.0 view source
5.3 Mineral Groups
Minerals are organized according to the anion or anion group (a group of atoms with a net negative charge, e.g., SO42–) they contain, because the anion or anion group has the biggest effect on the properties of the mineral. Silicates, with the anion group SiO44-, are by far the most abundant group in the crust and mantle. (They will be discussed in Section 5.4). The different mineral groups along with some examples of minerals in each group are summarized below.
5.3.1 Oxide Minerals: O2- Anion
Oxide minerals (Figure 5.14) have oxygen (O2–) as their anion. They don’t include anion groups with other elements, such as the carbonate (CO32–), sulphate (SO42–), and silicate (SiO44–) anion groups. The iron oxides hematite and magnetite are two examples that are important ores of iron. Corundum is an abrasive, but can also be a gemstone in its ruby and sapphire varieties. If the oxygen is also combined with hydrogen to form the hydroxyl anion (OH–), the mineral is known as a hydroxide. Some important hydroxides are limonite and bauxite, which are ores of iron and aluminum, respectively.

Figure 5.14: Oxide minerals include metal ore minerals, industrial minerals, and gemstones. Source: Karla Panchuk (2018) CC BY-NC-SA 4.0. Photos by R. Weller/ Cochise College. Click the image for photo sources.
5.3.2 Sulphide Minerals: S2- Anion
Sulphide minerals (Figure 5.15) include galena, sphalerite, chalcopyrite, and molybdenite, which are the most important ores of lead, zinc, copper, and molybdenum, respectively. Some other sulphide minerals are pyrite, bornite, stibnite, and arsenopyrite. Sulphide minerals tend to have a metallic sheen.

Figure 5.15: Sulphide minerals often have a metallic lustre and include metal ores. Source: Karla Panchuk (2018) CC BY-NC-SA 4.0. Photos by R. Weller/ Cochise College. Click the image for photo sources.
5.3.3 Sulphate Minerals: SO42- Anion Group
Many__ sulphate__ minerals form when sulphate-bearing water evaporates. A deposit of sulphate minerals may indicate that a lake or sea has dried up at that location. Sulphates with calcium include anhydrite, and gypsum (Figure 5.16). Sulphates with barium and strontium are barite and celestite, respectively. In all of these minerals, the cation has a +2 charge, which balances the –2 charge on the sulphate ion.

Figure 5.16: Sulphate minerals. Source: Karla Panchuk (2018) CC BY-NC-SA 4.0. Click the image for photo sources.
5.3.4 Halide Minerals: Anions from the Halogen Group
The anions in halides are the halogen elements including chlorine, fluorine, and bromine. Examples of halide minerals are cryolite, fluorite, and halite (Figure 5.17). Halide minerals are made of ionic bonds. Like the sulphates, some halides also form when mineral-rich water evaporates.

Figure 5.17: Halide minerals. Source: Karla Panchuk (2018) CC BY-NC-SA 4.0. Click the image for photo sources.
5.3.5 Carbonate Minerals: CO32- Anion Group
The __carbonate __anion group combines with +2 cations to form minerals such as calcite, magnesite, dolomite, and siderite (Figure 5.18). The copper minerals malachite and azurite are also carbonates. The carbonate mineral calcite is the main component of rocks formed in ancient seas by organisms such as corals and algae.

Figure 5.18: Carbonate minerals. Source: Karla Panchuk (2018) CC BY-SA 4.0. Photos by Rob Lavinsky, iRocks.com, CC BY-SA 3.0. Click the image for photo sources.
5.3.6 Phosphate Minerals: PO43- Anion
The apatite group of phosphate minerals (Figure 5.19, left) includes hydroxyapatite, which makes up the enamel of your teeth. Turquoise is also a phosphate mineral (Figure 5.19, right).

Figure 5.19: Phosphate minerals. Source: Karla Panchuk (2018) CC BY-NC-SA 4.0. Photos by R. Weller/ Cochise College. Click the image for photo sources.
5.3.7 Silicates (SiO44–)
The silicate minerals include the elements silicon and oxygen in varying proportions . These are discussed at length in Section 5.4.
5.3.8 Native Element Minerals
These are minerals made of a single element, such as gold, copper, silver, or sulphur (Figure 5.20).

Figure 5.20: Native element minerals are made up of a single element. Source: Karla Panchuk (2018) CC BY-SA 4.0. Click the image for photo sources.
Exercise: Mineral Groups
Minerals are grouped according to the anion part of the mineral formula, and mineral formulas are always written with the anion part last. For example, for pyrite (FeS2), Fe2+ is the cation and S– is the anion. This helps us to know that it’s a sulphide, but it is not always that obvious. Hematite (Fe2O3) is an oxide; that’s easy, but anhydrite (CaSO4) is a sulphate because SO42– is the anion, not O. Similarly, calcite (CaCO3) is a carbonate, and olivine (Mg2SiO4) is a silicate. Minerals with only one element (such as S) are native minerals, while those with an anion from the halogen column of the periodic table (Cl, F, Br, etc.) are halides. Provide group names for the following minerals:
| Mineral | Formula | Group |
|---|---|---|
| sphalerite | ZnS | |
| magnetite | Fe3O4 | |
| pyroxene | MgSiO3 | |
| anglesite | PbSO4 | |
| sylvite | KCl | |
| silver | Ag | |
| fluorite | CaF2 | |
| ilmenite | FeTiO3 | |
| siderite | FeCO3 | |
| feldspar | KAlSi3O8 | |
| sulphur | S | |
| xenotime | YPO4 |
5.4 Silicate Minerals
Silicon and oxygen bond covalently to create a silicate tetrahedron (SiO44-), which is a four-sided pyramid shape with oxygen at each corner and silicon in the middle (Figure 5.21). This structure is the building block of many important minerals in the crust and mantle. Silicon has a charge of +4, and oxygen has a charge of -2, so the total charge of the silicate anion is -4.
_](figures/05-minerals/figure-5-21.png)
Figure 5.21: The silica tetrahedron is the building block of all silicate minerals. Source: Karla Panchuk (2018) CC BY-SA 4.0. Modified after Helgi (2013) CC BY-SA 3.0 view source
In silicate minerals, these tetrahedra are arranged and linked together in a variety of ways, from single units to chains, rings, and more complex frameworks. In the rest of this section we will discuss the structures of the most common silicate minerals in Earth’s crust and mantle.
Exercise: Make a Tetrahedron
Download this PDF file with the tetrahedron pattern below. Cut around the outside of the shape (solid lines and dotted lines), and then fold along the solid lines to form a tetrahedron.
If you have glue or tape, secure the tabs to the tetrahedron to hold it together. If you don’t have glue or tape, make a slice along the thin grey line and insert the pointed tab into the slit.
If you’re feeling ambitious, make several tetrahedra and and use toothpicks through the corners to make the configurations discussed below.
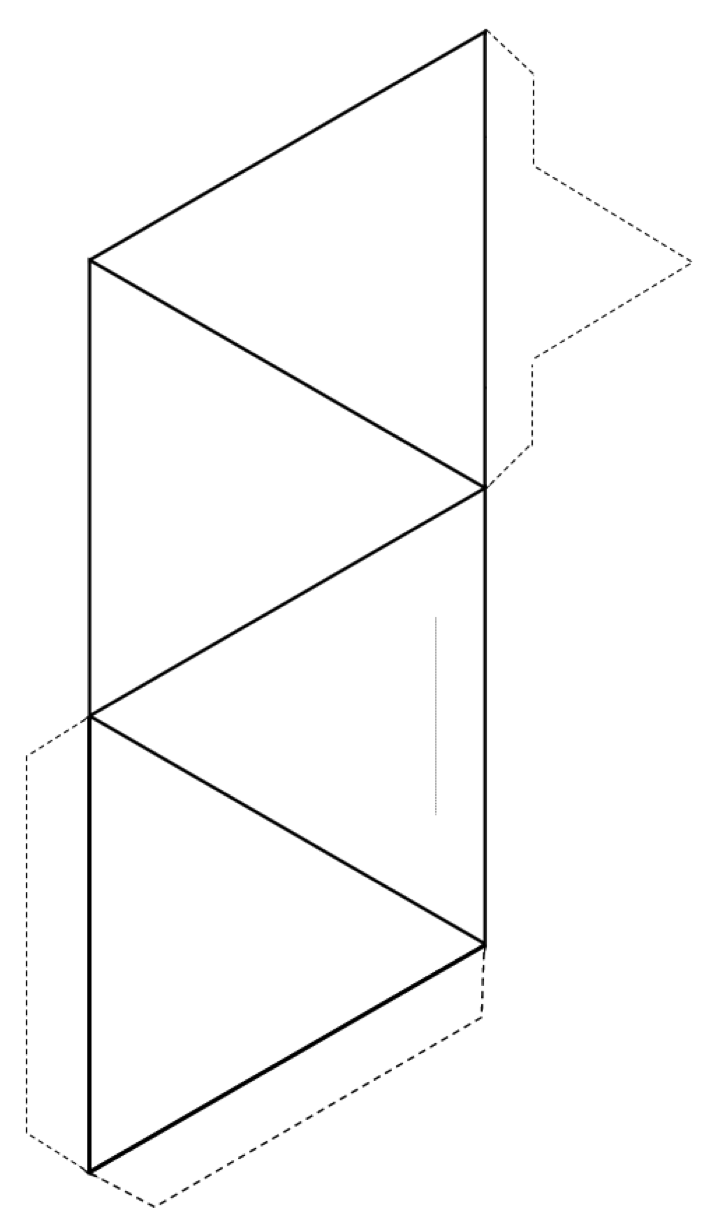](figures/05-minerals/figure-5-22.png)
Figure 5.22: Pattern for a tetrahedron. Source: Steven Earle (2015) CC BY 4.0 view source
5.4.1 Isolated Tetrahedra
The simplest silicate structure, that of the mineral olivine (Figure 5.23), is composed of isolated tetrahedra bonded to iron and/or magnesium ions (Figure 5.23 left). In olivine, the –4 charge of each silica tetrahedron is balanced by two iron or magnesium cations, each with a charge of +2. Olivine can be pure Mg2SiO4 or Fe2SiO4, or a combination of the two, written as (Mg,Fe)2SiO4. Magnesium and iron can substitute for each other because they both have a charge of +2, and they are similar in size. Magnesium cations have a radius of 0.73 Å, and iron cations have a radius of 0.62 Å.5
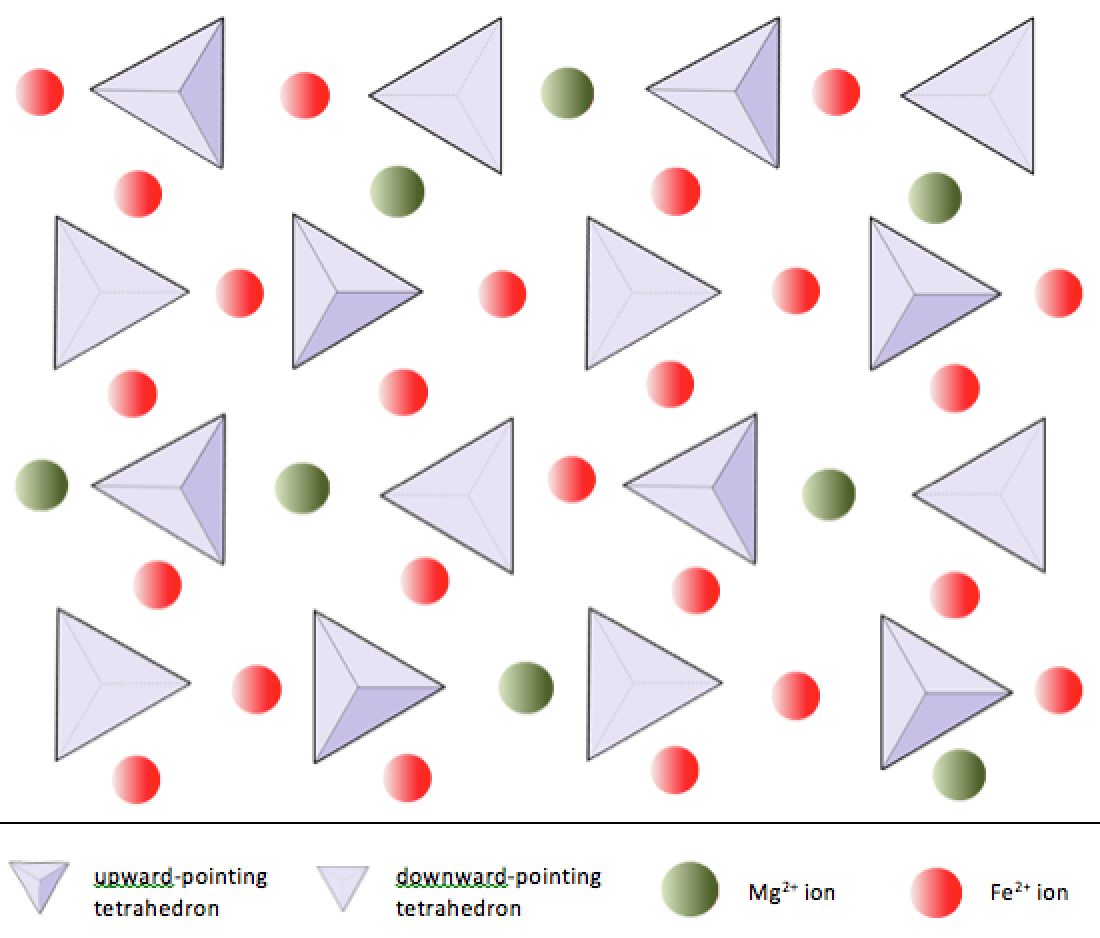. Click the image for photo sources._](figures/05-minerals/figure-5-23.png)
Figure 5.23: Olivine is a silicate mineral made of isolated silica tetrahedra bonded to Fe and Mg ions (left). Olivine crystals (centre) can often be found in the volcanic igneous rock called basalt (right). Source: Karla Panchuk (2018) CC BY-SA 4.0. Left- modified after Steven Earle (2015) CC BY 4.0 view source. Click the image for photo sources.
Although the iron and magnesium ions are similar in size, allowing them to substitute for each other in some silicate minerals, the common ions in silicate minerals have a wide range of sizes (Figure 5.24). Ionic radii are critical to the composition of silicate minerals, because the structure of the silicate mineral will determine the size of spaces available.
_](figures/05-minerals/figure-5-24.png)
Figure 5.24: The ionic radii in angstroms of some of the common ions in silicate minerals. Radii shown to scale. Notice that iron appears twice with two different radii. This is because iron can exist as a +2 ion (if it loses two electrons when it becomes an ion) or a +3 ion (if it loses three). Fe2+ is known as ferrous iron. Fe3+ is known as ferric iron. Source: Karla Panchuk (2017) CC BY 4.0. Modified after Steven Earle (2015) CC BY 4.0 view source
5.4.2 Chain Silicates
Pyroxene (Figure 5.25 bottom left) is an example of a single-chain silicate. The structure of chain silicates is shown in Figure 5.25 (top). In pyroxene__,__ silica tetrahedra form a chain because one oxygen from each tetrahedron is shared with the adjacent tetrahedron. This means there are fewer oxygens in the structure. This can be expressed as an oxygen-to-silicon ratio (O:Si). The O:Si is lower than in olivine (3:1 instead of 4:1), and the net charge per silicon atom is less (–2 instead of –4), because fewer cations are necessary to balance that charge.
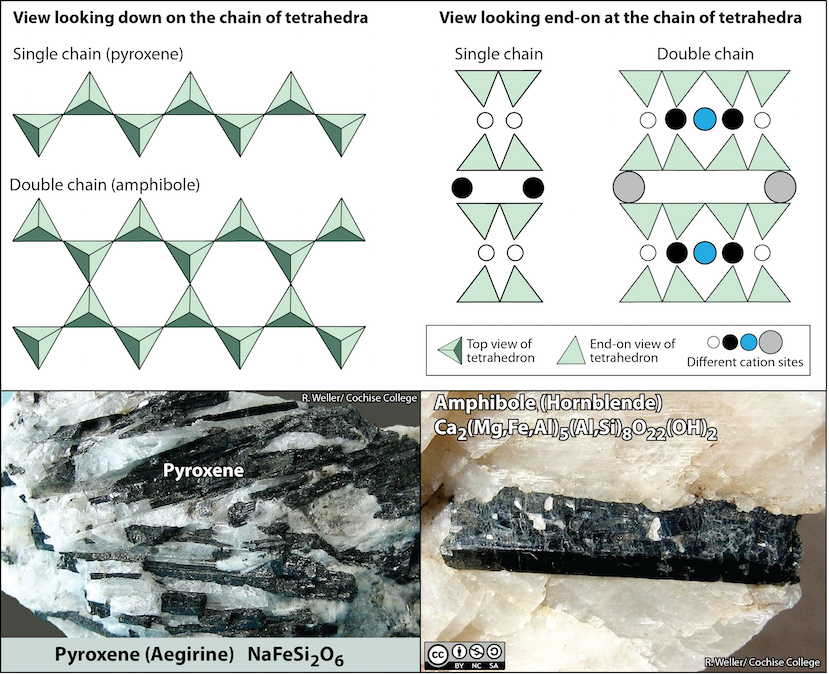
Figure 5.25: Chain silicate minerals. Top: Arrangement of silica tetrahedra in single and double chains. Bottom left: Pyroxene crystals (dark crystals) of the variety aegirine (acmite). Bottom right: Amphibole crystal (dark) of the variety hornblende. Source: Karla Panchuk (2018) CC BY-NC-SA 4.0. Top left- modified after Steven Earle (2015) CC BY 4.0. Top right- modified after Klein & Hurlbut (1993). Photos by R. Weller/ Cochise College. Click the image for sources.
Pyroxene compositions have the silica tetrahedra represented as SiO3 (e.g., MgSiO3, FeSiO3, and CaSiO36.) In other words, pyroxene has one cation for each silica tetrahedron (e.g., MgSiO3) while olivine has two (e.g., Mg2SiO4). The structure of pyroxene is more “permissive” than that of olivine, meaning cations with a wider range of ionic radii can fit into it. That’s why pyroxenes can have calcium cations (radius 1.00 Å) substitute for iron (0.63 Å) and magnesium (0.72 Å) .
In amphibole (Figure 5.25 bottom right), the silica tetrahedra are linked in a double chain that has an oxygen-to-silicon ratio lower than that of pyroxene, and hence still fewer cations are necessary to balance the charge. Amphibole is even more permissive than pyroxene and its compositions can be very complex, as shown by the formula for the hornblende group of amphibole minerals in Figure 5.25 (bottom right).
Exercise: Oxygen to Silicon Ratio
Figure 5.26 shows single chain and double chain structures. Count the number of tetrahedra versus the number of oxygen ions (yellow spheres) for each. Each tetrahedron has one silicon atom.
- Confirm for yourself that the ratio of silicon to oxygen in the single chain is 1:3.
- What is the O:Si for the double chain?
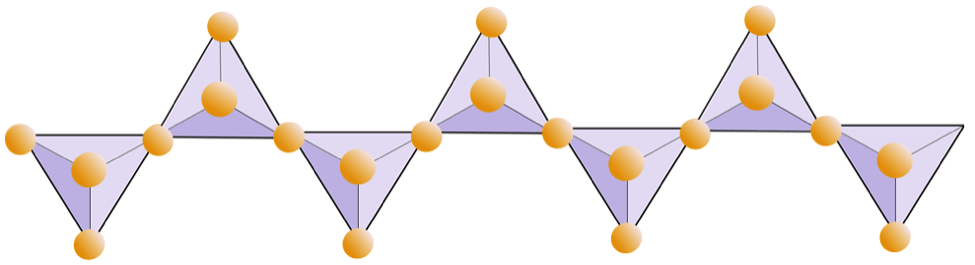/ [double chain](https://opentextbc.ca/geology/wp-content/uploads/sites/110/2015/06/diagram2.png)_](figures/05-minerals/figure-5-26.png)
Figure 5.26: Single and double chains of tetrahedra. Source: Karla Panchuk (2018) CC BY 4.0, modified after Steven Earle (2015) CC BY 4.0 single chain/ double chain
5.4.3 Sheet Silicates
In mica structures the silica tetrahedra are arranged in continuous sheets (Figure 5.27), where each tetrahedron shares three oxygen anions with adjacent tetrahedra. Because even more oxygens are shared between adjacent tetrahedra, fewer charge-balancing cations are needed for sheet silicate minerals. Bonding between sheets is relatively weak, and this accounts for the tendency of mica minerals to split apart in sheets (Figure 5.27 bottom right). Two common micas in silicate rocks are biotite (Figure 5.27 bottom left), which contains iron and/or magnesium, making it a dark mineral; andmuscovite (Figure 5.27 right), which contains aluminum and potassium, and is light in colour. All of the sheet silicate minerals have water in their structure, in the form of the hydroxyl (OH-) anion.
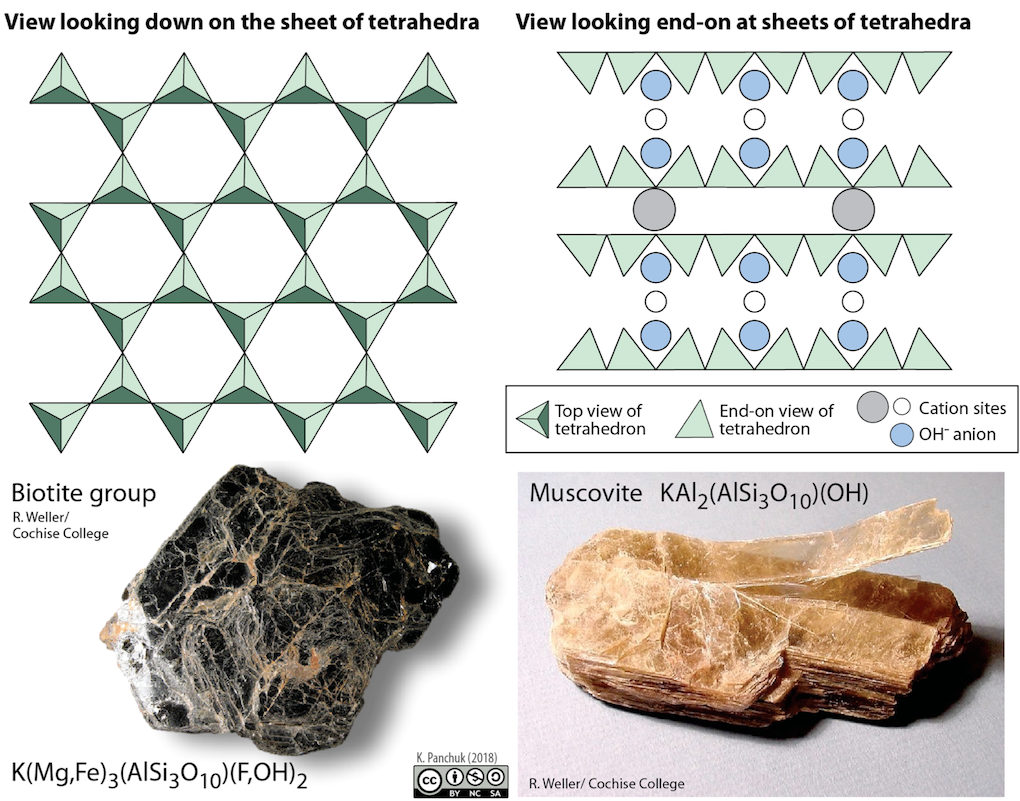
Figure 5.27: Micas are sheet silicates and split easily into thin layers along planes parallel to the sheets. Biotite mica (lower left) is has Fe and Mg cations. Muscovite mica (lower right) has Al and K instead. The muscovite mica shows how thin layers can split away in a sheet silicate. Source: Karla Panchuk (2018) CC BY-NC-SA 4.0. Top left- modified after Steven Earle (2015) CC BY 4.0. Top right- modified after Klein & Hurlbut (1993). Photos by R. Weller/ Cochise College. Click the image for sources.
Some sheet silicates typically occur in clay-sized fragments (i.e., less than 0.004 mm). These include the clay minerals kaolinite, illite, and smectite, which are important components of rocks and especially of soils.
5.4.4 Framework Silicates
In framework silicates, tetrahedra are connected to each other in three-dimensional structures rather than in two-dimensional chains and sheets.
5.4.4.1 Feldspar
Feldspars are a group of very abundant framework silicates in Earth’s crust. They include alumina tetrahedra as well as silicate tetrahedra. In alumina tetrahedra, there is an aluminum cation at the centre instead of a silicon cation.
Feldspars are classified using a ternary (3-fold) system with three end-members (“pure” feldspars). This system is illustrated with a triangular diagram that has each end-member at one corner (Figure 5.28). The distance along a side of the diagram represents the relative abundance of the composition of each end-member.
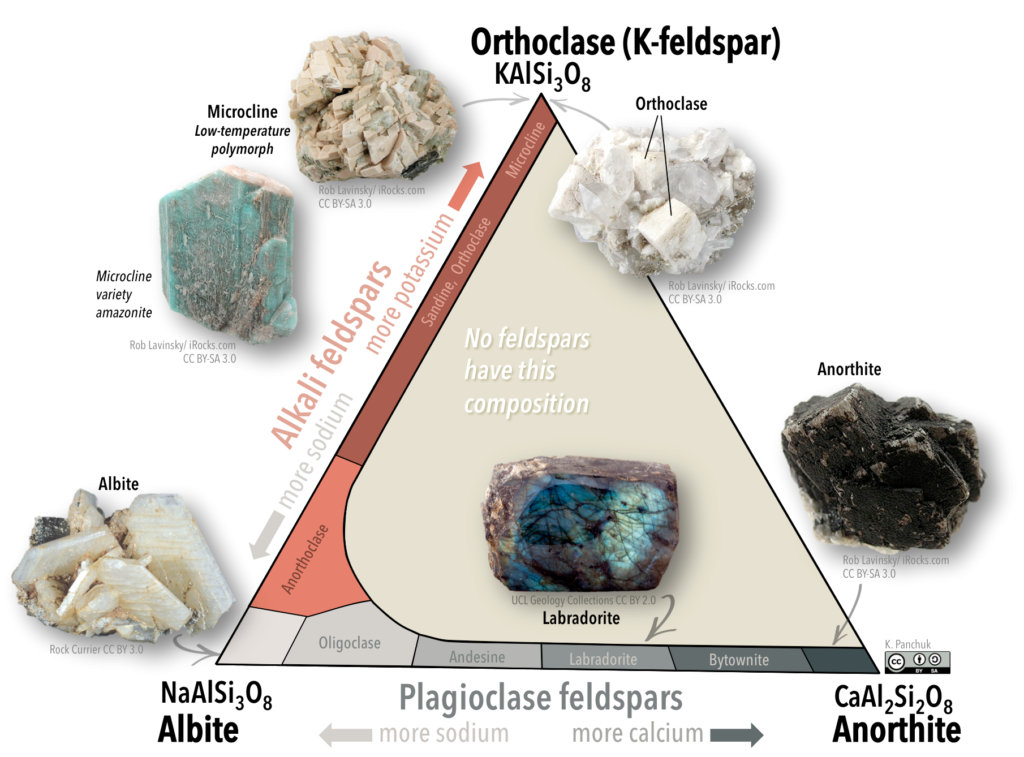
Figure 5.28: Ternary diagram showing the feldspar group of framework silicate minerals. Alkali feldspars are those with compositions ranging between albite (with a Na cation) and orthoclase and its polymorphs (with a K cation. Plagioclase feldspars are those with compositions ranging between albite and anorthite (with a Ca cation). Source: Karla Panchuk (2018) CC BY-SA 4.0. Ternary diagram modified after Klein & Hurlbut (1993). Click the image for photo sources and a ternary diagram without mineral images.
One end-member is potassium feldspar (also referred to as K-feldspar), which has the composition KAlSi3O8. Depending on the temperature and rate of cooling, K-feldspar can occur as one of three polymorphs: orthoclase, sanidine, or microcline. Another end member is albite, which has sodium instead of potassium (formula NaAlSi3O8).As is the case for iron and magnesium in olivine, there is a continuous range of compositions (referred to as a solid-solution series) between albite and orthoclase. Feldspars in this series are referred to as alkali feldspars. Potassium cations are much larger than sodium cations (1.37 Å versus 0.99 Å, respectively), so high temperatures are required to form alkali feldspars with intermediate compositions.
The third end-member is anorthite and it has calcium instead of potassium or sodium (formula CaAl2Si3O8). Feldspars in the solid-solution series between albite and anorthite are called plagioclase feldspars. Calcium and sodium cations are nearly the same size (1.00 Å and 0.99 Å, respectively), so from that perspective it makes sense that they substitute readily for each other, and that any intermediate compositions between CaAl2Si3O8 and NaAlSi3O8 can exist. However, calcium and sodium ions don’t have the same charge (Ca2+ versus Na+), making it surprising that they substitute so easily. The difference in charge is accommodated by substituting some Al3+ for Si4+. Albite has one Al and three Si in its formula, while anorthite is has two Al and two Si. Plagioclase feldspars of intermediate composition also have intermediate proportions of Al and Si.
5.4.4.2 Quartz
Quartz (SiO2; Figure 5.29) contains only silica tetrahedra. In quartz, each silica tetrahedron is bonded to four other tetrahedra (with an oxygen shared at every corner of each tetrahedron), making a three-dimensional framework. As a result, the ratio of silicon to oxygen is 1:2. Because the one silicon cation has a +4 charge and the two oxygen anions each have a –2 charge, the charge is balanced. There is no need to add cations to balance the charge. The hardness of quartz and the fact that it breaks irregularly (notice the bottom of the crystal in Figure 5.29 right) and not along smooth planes result from the strong covalent/ionic bonds characteristic of the silica tetrahedron.
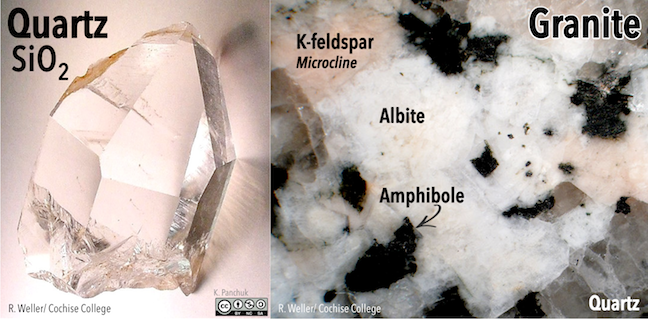
Figure 5.29: Quartz is another silicate mineral with a three-dimensional framework of silica tetrahedra. Sometimes quartz occurs as well-developed crystals (left), but it also occurs in common rocks such as granite (right). In addition to quartz, the granite contains potassium feldspar, albite, and amphibole. Source: Karla Panchuk (2018) CC BY-NC-SA 4.0. Photos by R. Weller/ Cochise College. Click the image for photo sources.
5.5 How Minerals Form
The following criteria are required for mineral crystals to grow:
- The elements needed to make the mineral crystals must be present in sufficient abundance and appropriate proportions.
- The physical and chemical conditions must be favourable.
- There must be sufficient time for the atoms to become arranged into a lattice.
Physical and chemical conditions include factors such as temperature, pressure, amount of oxygen available, pH, and the presence of water. The presence of water makes it easier for ions to move to where there are needed, and can lead to the formation of larger crystals over shorter time periods, as with the gypsum crystals at the beginning of this chapter. Time is one of the most important factors because it takes time for atoms to line themselves up into an orderly structure. If time is limited, the mineral grains may remain very small.
Most of the minerals that make up the rocks in the crust and mantle formed through the cooling of molten rock, known as magma. At the high temperatures that exist deep within Earth, some geological materials are liquid. As magma rises up through the crust, either by volcanic eruption or by more gradual processes, it cools and minerals crystallize. When cooling is rapid and many crystals form at once, only small mineral grains will form before the rock becomes solid. The resulting rock will be fine-grained (i.e., crystals less than 1 mm). When cooling is slow, or when few crystals are growing at a time, relatively large crystals will develop.
Minerals can also form in several other ways:
- Precipitation from a solution (e.g., from hot water flowing underground, or when evaporation concentrates ions in a lake or inland sea)
- Precipitation from a gas (e.g., from vents releasing volcanic gases)
- Metamorphism: solid minerals react with each other under high pressures and temperatures, and new minerals are formed.
- Weathering: minerals unstable at Earth’s surface are chemically altered by surface processes.
- Organic formation: organisms build shells (primarily of calcite or aragonite), and teeth and bones (primarily of apatite).
5.6 Mineral Properties
Minerals are universal. A crystal of hematite on Mars will have the same properties as one on Earth, and the same as one on a planet orbiting another star. That’s good news for geology students who are planning interplanetary travel, because they can use the same properties to identify minerals anywhere. That doesn’t mean that it’s easy, however. Identification of minerals takes practice. Some of the mineral properties that are useful for identification are colour, streak, lustre, hardness, habit, cleavage or fracture, and density.
5.6.1 Colour
Some minerals have distinctive colours that useful as diagnostic criteria.The mineral sulphur (Figure 5.30 left) is always a characteristic bright yellow. For other minerals, colour might vary. Hematite is an example of a mineral for which colour is not necessarily diagnostic. In some forms hematite is a deep dull red (a fairly unique colour), but in others it is a metallic silvery black (Figure 5.30, right).

Figure 5.30: Colour is a useful diagnostic property for sulphur (left) and for some types of hematite (right) because the yellow and dark red colours are unique to those minerals. In contrast, silvery metallic forms of hematite are similar in appearance to many other minerals._ Source: Karla Panchuk (2018) CC BY-NC-SA 4.0. Photos by R. Weller/ Cochise College. Click the image for photo sources._
For other minerals, the problem is that a single mineral can have a wide range of colours. The colour variations can be the result of varying proportions of trace elements within the mineral, or structural defects within the crystal lattice. In the case of quartz (Figure 5.31), milky quartz gets its white colour from millions of tiny fluid-filled cavities. Smoky quartz gets its grey colour from structural damage caused by natural radiation. Amethyst and citrine get their colours from trace amounts of iron, and rose quartz gets its pink hue from manganese.

Figure 5.31: The many colours of quartz.Quartz can be colourless, milky, a greyish smoky colour, purple, yellow, and pink. Source: Karla Panchuk (2018) CC BY-NC-SA 4.0. Photos by R. Weller/ Cochise College. Click the image for photo sources.
5.6.2 Streak
The colour of a mineral is what you see when light reflects off the surface of the sample. One reason that colour can be so variable is that the surface textureis variable. A way to get around this problem is to grind a small amount of the sample to a powder and observe the colour of the powder. This colour is the mineral’s streak. The mineral can be powdered by scraping the sample across a piece of unglazed porcelain called a streak plate (Figure 5.32). In Figure 5.32, two samples of hematite have been scraped across the streak plate. Even though one sample is metallic and the other is deep red, both have a similar reddish-brown streak.

Figure 5.32: Hematite leaves a distinctive reddish-brown streak whether the sample is metallic or deep red. Source: Karla Panchuk (2015) CC BY 4.0
Streak is an especially helpful property when minerals look similar. In Figure 5.33 all of the minerals are dark in colour, with varying degrees of metallic sheen. The streaks of these minerals are much more distinctive.

Figure 5.33: Similar dark-grey minerals with varying degrees of metallic sheen leave different colours of streaks. The minerals are from upper left clockwise: hematite, magnetite, sphalerite, and galena. Source: Karla Panchuk (2015) CC BY 4.0
5.6.3 Lustre
Lustre is the way light reflects off the surface of a mineral, and the degree to which it penetrates into the interior. The key distinction is between metallic and non-metallic lustre. Light does not pass through metals, and that is the main reason they look metallic (e.g., the hematite on left of Figure 5.32). Even a thin sheet of metal — such as aluminum foil — will be not permit light to pass through it. Many non-metallic minerals may look as if light will not pass through them, but if you look closely at a thin slice of the mineral you will see that the mineral is translucent or transparent.
If a non-metallic mineral has a shiny, reflective surface, it is said to have a glassy lustre. The quartz crystals in Figure 5.31 are examples of minerals with glassy lustre. If the mineral surface is dull and non-reflective, it has an earthy lustre (like the hematite on the right of Figure 5.32). Other types of non-metallic lustres are silky, pearly, and resinous. Lustre is a good diagnostic property because most minerals will always appear either metallic or non-metallic, although as Figure 5.31 shows, there are exceptions.
5.6.4 Hardness
One of the most important diagnostic properties of a mineral is its hardness. In practical terms, hardness determines whether or not a mineral can be scratched by a particular material.
In 1812 German mineralogist Friedrich Mohs came up with a list of 10 minerals representing a wide range of hardness, and numbered them 1 through 10 in order of increasing hardness (Figure 5.34, horizontal axis). While each mineral on the list is harder than the one before it, the measured hardness (vertical axis) is not linear. Notice that apatite is about three times harder than fluorite, and diamond is three times harder than corundum.
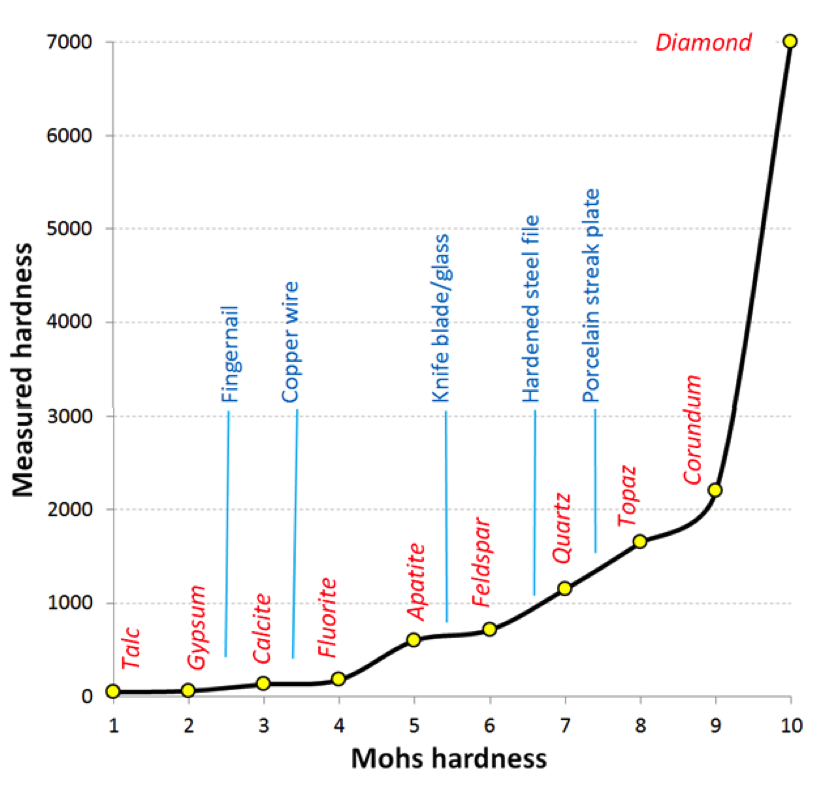_](figures/05-minerals/figure-5-34.png)
Figure 5.34: Minerals and reference materials in the Mohs scale of hardness. The measured hardness values are Vickers Hardness numbers._ Source: Steven Earle (2015) CC BY 4.0 view source_
Some commonly available reference materials are also shown on this diagram, including a typical fingernail7 (2.5), a piece of copper wire (3.5), a knife blade or piece of window glass (5.5), a hardened steel file (6.5), and a porcelain streak plate (7). These are tools that a geologist can use to measure the hardness of unknown minerals: if you have a mineral that you can’t scratch with your fingernail, but you can scratch with a copper wire, then its hardness is between 2.5 and 3.5. The minerals themselves can be used to test other minerals.
5.6.5 Crystal Habit
When minerals form within rocks, there is a possibility that they will form in distinctive crystal shapes if they are not crowded out by other pre-existing minerals. Every mineral has one or more distinctive crystal habits determined by their atomic structure, although it is not that common in ordinary rocks for the shapes to be obvious.
Quartz, for instance, will form six-sided prisms with pointed ends (Figure 5.35 left), but this typically happens only when it crystallizes from a hot water solution within a cavity in an existing rock. Pyrite can form cubic crystals (Figure 5.35 centre), but can also form crystals with 12 faces, known as dodecahedra. The mineral garnet also forms many-sided crystals with an over-all rounded shape (Figure 5.35 right).

Figure 5.35: Hexagonal prisms of quartz (left), intergrown cubic crystals of pyrite (centre), and 24-sided crystals of garnet (right). Source: Karla Panchuk (2018) CC BY-NC-SA 4.0. Photos by R. Weller/ Cochise College. Click the image for photo sources.
Some of the terms that are used to describe habit include bladed, botryoidal (grape-like), dendritic (branched), drusy (an encrustation of crystals), equant (similar size in all dimensions), fibrous, platy, prismatic (long and thin), and stubby.
5.6.6 Cleavage and Fracture
Cleavage and fracture describe how a mineral breaks. These characteristics are the most important diagnostic features of many minerals, and often the most difficult to understand and identify. Cleavage is what we see when a mineral breaks along a plane or planes, while fracture is an irregular break. Some minerals tend to cleave along planes at various fixed orientations. Some, like quartz, do not cleave at all, only fracture. Minerals that have cleavage can also fracture along surfaces that are not parallel to their cleavage planes.
The way minerals break is determined by the arrangement of atoms within them, and more specifically by the orientation of weaknesses within their crystal lattice. Graphite and mica break off in parallel sheets (Figure 5.36).
_](figures/05-minerals/figure-5-36.png)
Figure 5.36: One direction of cleavage (basal cleavage). Left: Schematic of basal cleavage. Right: Muscovite showing basal cleavage. The white dashed line marks the edge of the cleavage plane. Source: Karla Panchuk (2018) CC BY-SA 4.0. Cleavage diagram modified after M.C. Rygel (2010) CC BY-SA 3.0 view source
Other minerals have two directions of cleavage, classified as two directions at 90° (Figure 5.37 top) and two directions not at 90° (Figure 5.37 bottom). While the diagrams of planes on the left of Figure 5.37 make this difference clear, it may be less obvious in practice. The minerals in Figure 5.37 both have two planes of cleavage that are very close to 90°. The white dashed lines mark the edges of the planes, as with Figure 5.36. See if you can find the planes repeated in the images. The images are close-up views of the minerals, only a few cm across. Sometimes you must look very carefully to find cleavage planes.
_](figures/05-minerals/figure-5-37.png)
Figure 5.37: Two directions of cleavage. Top: Two directions at 90° in pyroxene. Bottom: two directions not at 90° in plagioclase feldspar. Edges of cleavage planes marked with dashed lines. Source: Karla Panchuk (2018) CC BY-SA 4.0. Cleavage diagrams modified after M.C. Rygel (2010) CC BY-SA 3.0 view source
Some minerals have many directions of cleavage. Figure 5.38 shows minerals with three directions of cleavage. Halite (Figure 5.38 top) has three directions at 90° and calcite (Figure 5.38 bottom) has three directions not at 90°.
_](figures/05-minerals/figure-5-38.png)
Figure 5.38: Three directions of cleavage. Top: Three directions at 90° in halite. Bottom: Three directions not at 90° in calcite. Source: Karla Panchuk (2018) CC BY-SA 4.0. Cleavage diagrams modified after M.C. Rygel (2010) CC BY-SA 3.0 view source
There are a few common difficulties that students encounter when learning to recognize and describe cleavage. One is that it might be necessary to look very closely at a sample to see mineral cleavage. The key features in Figure 5.37 are only cm or mm in scale. If crystals are very small, it may not be possible to see cleavage at all. Another issue is that sometimes cleavage is present, but it is poor, meaning the cleavage surface isn’t perfectly flat. Finally it can be difficult to know whether a flat surface on a crystal is a cleavage plane, a crystal face, or simply a surface that happens to be flat. Cleavage planes tend to repeat themselves at different depths throughout the mineral, so if you are unsure whether the surface you are looking at is a cleavage plane, try rotating the mineral in bright light. If cleavage is present, you will generally find that, for a given cleavage direction, all of the cleavage surfaces will glint in the light simultaneously. Crystal faces will also glint in light, but they do not repeat themselves at depth throughout the mineral. The best way to overcome all of these problems is to look at lots of examples. It’s worth it to be able to identify cleavage and fracture, because cleavage is a reliable diagnostic property for most minerals.
5.6.7 Density
Density is a measure of the mass of a mineral per unit volume, and it is a useful diagnostic tool in some cases. Most common minerals, such as quartz, feldspar, calcite, amphibole, and mica, are of average density (2.6 to 3.0 g/cm3), and it would be difficult to tell them apart on the basis of their density. On the other hand, many of the metallic minerals, such as pyrite, hematite, and magnetite, have densities over 5 g/cm3. If you picked up a sample of one of these minerals, it would feel much heavier compared to a similarly sized sample of a mineral with average density. A limitation of using density as a diagnostic tool is that one cannot assess it in minerals that are a small part of a rock with other minerals in it.
5.6.8 Other properties
Several other properties are useful for identification of some minerals. Some of these are:
- Calcite reacts with dilute acid and will give off bubbles of carbon dioxide.
- Magnetite is strongly magnetic, and some other minerals are weakly magnetic.
- Sphalerite ((Zn,Fe)S) gives off a smell of sulphur when drawn across a streak plate.
- Halite tastes salty.
- Talc feels soapy to the touch.
- Plagioclase feldspar has striations (parallel razor-thin lines etched on the surface) and some varieties show a play of colours when light hits them at the right angle (see the labradorite in Figure 5.28).
5.7 Summary
The topics covered in this chapter can be summarized as follows:
5.7.1 Atoms
An atom is made up of protons and neutrons in the nucleus, and electrons arranged in energy shells around the nucleus. The first shell holds two electrons, and outer shells hold more. Atoms strive to have eight electrons in their outermost shell (or two for H and He). Atoms gain, lose, or share electrons to achieve this. In so doing they become either positively charged cations (if they lose electrons) or negatively charged anions (if they gain them).
5.7.2 Bonding and Lattices
The main types of bonding in minerals are ionic bonding (electrons transferred) and covalent bonding (electrons shared). Some minerals have metallic bonding or weak Van der Waals forces. Minerals form in three-dimensional lattices. The configuration of the lattices and the type of bonding within help determine mineral properties.
5.7.3 Mineral Groups
Minerals are grouped according to the anion part of their formula. Some common types are: oxides, sulphides, sulphates, halides, carbonates, phosphates, silicates, and native minerals.
5.7.4 Silicate Minerals
Silicate minerals are the most common minerals in Earth’s crust and mantle. They all have silica tetrahedra (four oxygens surrounding a single silicon atom) arranged in different structures (chains, sheets, etc).
5.7.5 How Minerals Form
Most minerals in the crust form from the cooling and crystallization of magma. Some form from hot water solutions, during metamorphism or weathering, or through organic processes. More rarely, minerals precipitate directly from a gas, such as at a volcanic vent.
5.7.6 Mineral Properties
Some of the important properties for mineral identification include hardness, cleavage/fracture, density, lustre, colour, and streak colour.
5.8 Chapter Review Questions
What is the electrical charge of a proton? A neutron? An electron? What are their relative masses?
Explain how the need for an atom’s outer shell to be filled with electrons contributes to bonding.
Why are helium and neon non-reactive?
What is the difference in the role of electrons in an ionic bond compared to a covalent bond?
How do cations differ from anions?
What chemical feature is used in the classification of minerals into groups?
Name the mineral group for the following minerals:
- calcite
- biotite
- pyrite
- gypsum
- galena
- orthoclase
- hematite
- graphite
- magnetite
- quartz
- fluorite
- olivine
What is the net charge on an unbonded silica tetrahedron?
What allows magnesium to substitute freely for iron in olivine?
How are the silica tetrahedra structured differently in pyroxene and amphibole?
Why is biotite called a ferromagnesian mineral, while muscovite is not?
What are the names and compositions of the two end-members of the plagioclase series?
Why does quartz have no additional cations (other than Si+4)?
Why is colour not necessarily a useful guide to mineral identification?
You have an unknown mineral that can scratch glass but cannot scratch a porcelain streak plate. What is its approximate hardness?
5.9 Answers to Chapter Review Questions
Charges: proton: +1, neutron: 0, electron: -1, Masses: proton: 1, neutron: 1, electron: almost 0.
The element’s atomic number will determine the extent to which its outer layers are populated with electrons. If the outer shell is not quite full, the atom may gain electrons to fill them and become an anion (negative charge). If the outer shell has only a few electrons, it may lose them and become a cation (positive charge). Cations and anions attract each other to form molecules with ionic bonding.
Helium and neon (and the other noble gases) have complete outer shells and therefore no tendency to form ionic bonds.
Electrons are transferred from one atom to another to form an ionic bond. Electrons are shared between atoms to form a covalent bond.
An anion has a negative charge and a cation has a positive charge.
Minerals are classified into groups based on their anion or anion group.
Name the mineral group for the following minerals:
- calcite: CaCO3 carbonate
- biotite: silicate
- pyrite: FeS2 sulphide
- gypsum: CaSO4 sulphate
- galena: PbS sulphide
- orthoclase: KAlSi3O8 silicate
- hematite: Fe2O3 oxide
- graphite: C native
- magnetite: Fe3O4 oxide
- quartz: SiO2 silicate
- fluorite: CaF2 halide
- olivine: MgSiO4 silicate
An unbonded silica tetrahedron has one Si ion (+4 charge) and 4 oxygens (-2 charge each) so the overall charge is 4 – 8 = -4 for SiO4-4
Magnesium can substitute freely for iron in olivine and several other minerals because they have similar charges (+2) and similar ionic radii.
Pyroxene is made up of single chains of tetrahedra while amphibole is made up of double chains.
The two end-members of the plagioclase series are Albite (NaAlSi3O8) and Anorthite (CaAl2Si2O8)
In quartz each silica tetrahedron is bonded to four other tetrahedra, and because oxygens are shared at each bond the overall ratio is silicon (+4) to two oxygens (2 x -2 = -4), which is balanced.
Some minerals have distinctive colours, but many have a wide range of colours due to differing impurities.
Glass has a Mohs hardness of about 5.5 while porcelain is close to 6.5. The mineral is between these two, so it must be close to 6.
5.10 References
Nickel, E. H. (1995). The Definition of a Mineral. The Canadian Mineralogist 33, 698-690. Read paper
Williams, P. (2010, July 28). Deadliest place on Earth? Surviving Cueva de los Cristales - The Giant Crystal Cave. Visit website
Klein, C. & Hurlbut, C. S., Jr. (1993)._Manual of Mineralogy (after J. D. Dana). _New York, NY: John Wiley & Sons, Inc.
You can remember that a cation is positive by remembering that a cat has paws (paws sounds like “pos” in “positive”). You could also think of the “t” in “cation” as a plus sign.↩︎
Å stands for Ångstrom, a unit commonly used to express atomic-scale dimensions. One angstrom is 10–10 m or 0.0000000001 m.↩︎
The variation in composition can also be written as (Mg,Fe,Ca)SiO3, where the elements in the brackets can be present in any proportion. ↩︎
Note that artificial fingernails may be much harder than natural fingernails. Some materials used for artificial nails are harder than quartz.↩︎